前言
这节课使我们讲解上下文无关语言的最后一节了。但是往后的课程的内容中我们会不时地参考上下文无关语言,就行正则语言那样。
本节课的第一部分我们讲下推自动机的计算模型,它为了我们提供了可供选择的基于CFG的上下文无关语言的定义描述。第二部分我们谈一下至今都还未讨论过的一些上下文无关语言的属性,而且他们有助于理解下推自动机。
知识点
下推自动机
下推自动机(PDA)的计算模型本质上就是一个带有栈的NFA。正如我们将看到,PDA所识别的语言类正是上下文无关语言类,它提供了一个很有用的手段来推理这种语言类。
一些简单的例子
我们先来看一个PDA的简单例子,表达形式如图11.1的状态图所示。这个状态图看起来和NFA或者DFA的有点区别,因为它包含了一种操作栈的指令,但是基本思路是一样的。标有输入符号或者$\varepsilon$的转移表示我们读取了一个符号或者采用了$\varepsilon$-转移,就像一个NFA;标有$(\uparrow ,a)$的转移表示我们将符号$a$推入栈中;标有$(\downarrow ,a)$的转移表示我们将符号$a$弹出栈外。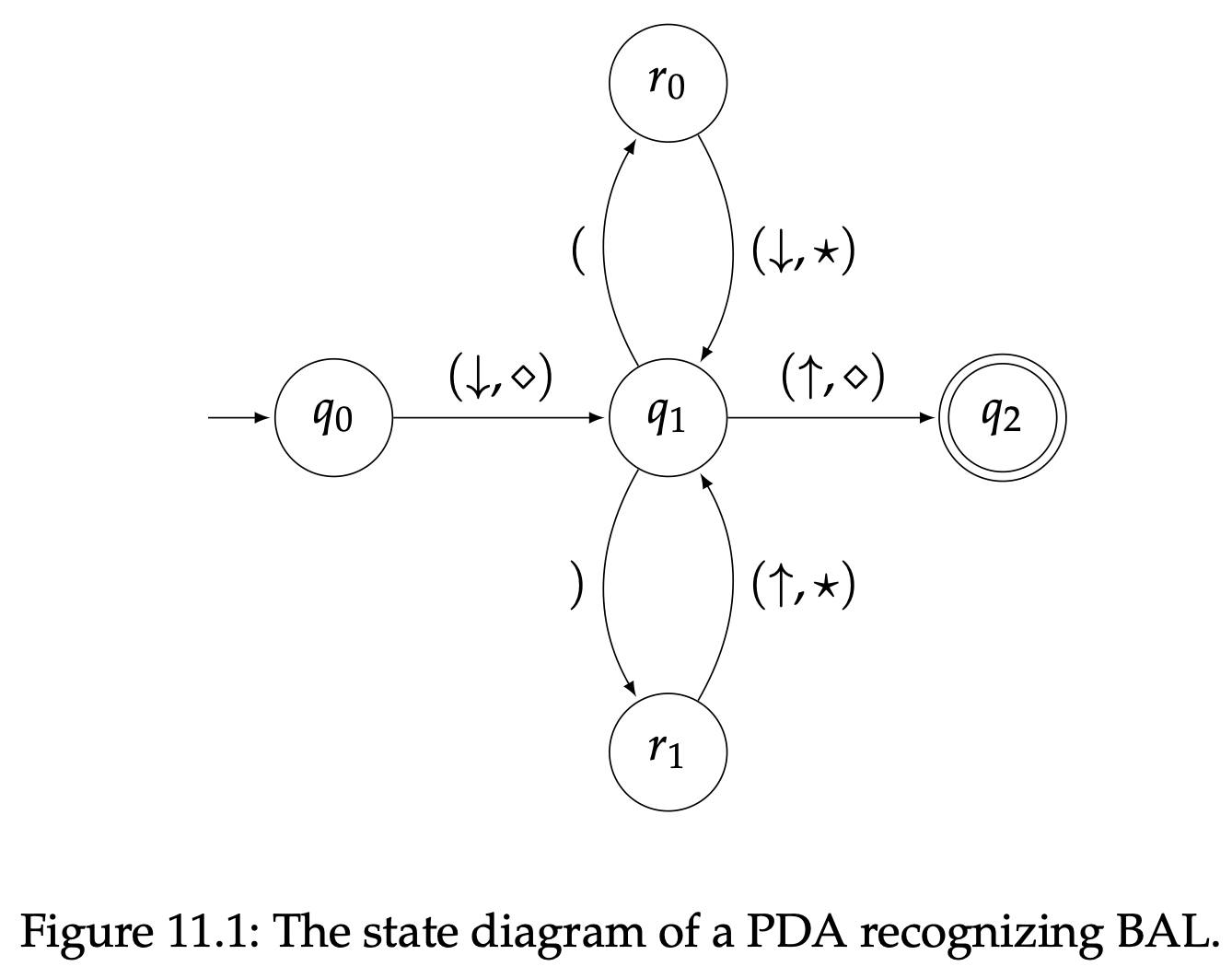
这样,图11.1中PDA $P$阐述的运行方式是首先将符号$\diamondsuit$推入栈中(我们假设栈一开始是空的)然后进入状态$q_1$(此时没有从输入中读取符号)。从状态$q_1$可以读取一个左括号“(”移动到状态$r_0$或者读取一个右括号“)”移动到状态$r_1$。想要回到状态$q_1$就一定要在栈中推入符号$\star$(对应我们读取一个左括号之后)或者弹出符号$\star$(对应我们读取一个右括号之后)。最后为了从$q_1$到达接受状态$q_2$,我们必须弹出栈中的符号$\diamondsuit$。注意一个符号能被弹出栈外仅当它处在栈顶的时候。
不难看出这个PDA所识别的语言是括号配对语言BAL;很明显这个PDA会根据输入字符串执行要求的推入和弹出操作后进入接受状态,并且读取完输入字符串。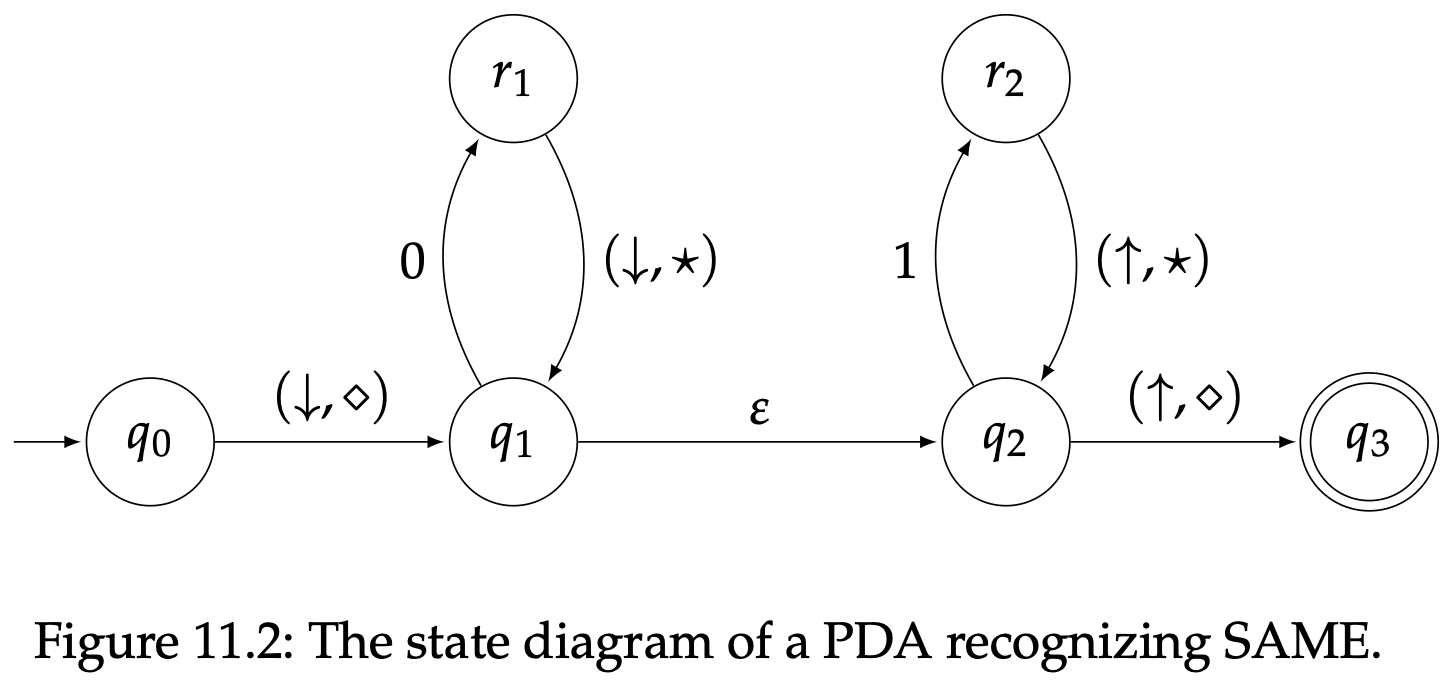
第二个例子图11.2中。这个PDA识别的语言是
这个情况下栈就被用来当一个计数器:我们为每个0推入一个星号,就得为每个1弹出一个星号,通过检测“栈底的标记”$\diamondsuit$来判断是否两种读入的符号数量相等。
下推自动机的定义
下推自动机模型的正式定义和非确定性有限自动机类似,除了PDA需要指定一个栈的符号表和修改转移函数的形式加入栈操作。
在我们看定义之前,让我们引入一些对于我们讨论栈操作有帮助的概念。对于任意字母表$\Gamma$,我们用它来当做栈的字母表,栈的操作字母表$\updownarrow\Gamma$的定义是
字母表$\updownarrow\Gamma$代表所有使用字母表$\Gamma$的可能的栈操作;对于每个$a\in\Gamma$,符号$(\downarrow , a)$代表将$a$推入栈中,符号$(\uparrow ,a)$代表将$a$弹出栈外。
定义11.2. 一个下推自动机(PDA)是一个6-元组
其中$Q$是一个有限非空状态集合,$\Sigma$是一个字母表(输入字母表),$\Gamma$也是一个字母表(栈字母表),两个字母表必须满足$\Sigma \cap \updownarrow \Gamma=\varnothing$,$\delta$是形式为
的函数,其中$q_0\in Q$是初始状态,$F\subseteq Q$是一个接受状态集合。
上面这个转移函数执行转移使用的符号都在集合$\Sigma\cup\updownarrow\cup\{ \varepsilon \}$中,我们能选择的操作是读取一个$\Sigma$中的符号、往栈里推入一个$\Gamma$中的符号、往栈外弹出一个$\Gamma$中的符号或者执行一个$\varepsilon$-转移。
有效的栈操作字符串
在我们讨论PDA接受输入的正式定义前,先来思考一下什么是有效的栈操作序列。已知一个任意栈字母表$\Gamma$,让$\updownarrow\Gamma$表示栈操作字母表。
我们来看一个字符串$v\in (\updownarrow\Gamma)^{*}$,它可能是一个有效的栈操作序列,也可能不是,假设我们从左往右读取它,而且栈一开始是空的。如果一个字符串代表一个有效栈操作序列,我们成它为有效栈字符串;如果一个字符串不能代表一个有效栈操作序列;我们成它为无效栈字符串。
比如,如果$\Gamma=\{0,1\}$,那么这些字符串是有效栈字符串:
在第一种情况中栈的变化就像这样(最左侧的符号表示栈顶元素):
第二种情况也是类似的,只不过最后栈没有清空:
另外,这里还有一些无效栈字符串:
第一种情况我们先推入了一个0,再推入一个1,完成之后,我们尝试先把0弹出,但这时候0不是栈顶元素(1才是)。第二种情况中最后一个操作符号有问题,因为它在栈空的时候尝试从栈中弹出一个1。
基于字母表$\updownarrow\Gamma$并且由有效栈字符串组成的语言是一个上下文无关语言。为了弄明白这个,我们先考虑一种有效栈字符串的语言,它的所有字符串的最后一个操作符号都将栈清空。比如,(11.5)中的第一个序列就清空了栈,第二个却没有。我们可以模仿括号配对语言的CFG来为这个语言构造一个CFG,但是每个符号我们要想象成不同类型的括号。
具体一点,让我们定义一个CFG $G$,它的规则如下:
其中每个符号$a\in\Gamma$,还包含一条规则$S\rightarrow\varepsilon$。这个CFG生成的是一个基于栈字母表$\Gamma$的有效栈字符串语言,最后栈是清空状态。
如果我们丢掉-最后一个操作后栈为空-这个要求,那我们仍然能得到一个上下文无关语言。这是因为这个语言是上一段中CFG所生成语言的前缀,而上下文无关语言在前缀操作下是闭合的。
定义PDA的接受输入
接着我们来思考一个PDA $P$接受一个或者拒绝一个字符串的$w$的定义。
定义11.2. 已知$P=(Q,\Sigma,\Gamma,\delta,q_0,F)$是一个PDA,$w\in\Sigma^{*}$是一个字符串。PDA $P$接受字符串仅当存在一个自然数$m\in\mathbb{N}$,存在一个状态序列$r_0,…,r_m$和序列
满足以下四个条件:
- $r_0=q_0$并且$r_m\in F$。
- 对于每个$k\in\{0,…,m-1\}$有$r_{k+1}\in\delta(r_k,a_{k+1})$。
- 通过从$a_1,…,a_m$中移除每个字母表$\updownarrow\Gamma$的符号,得到输入字符串$w$。
- 通过从$a_1,…,a_m$中移除每个字母表$\Sigma$的字符,得到一个有效栈字符串。
如果$P$不接受$w$,那么$P$就会拒绝$w$。
这个定义中大部分都是很浅显的。为了让$P$接受$w$,一定存在一个状态序列,在状态转移中同时满足输入字符串和转移函数。此外,栈的使用必须满足要求,也就是第四个条件必须满足。
一如既往,对于一个PDA $P$,我们使用$L(P)$来表示$P$所识别的语言,它的所有字符串都被$P$接受。
PDA状态图的一些简写表达
有时候PDA状态图的简写会很用,它可以用来表示一个单一的状态转移序列。特别是,如果一个转移标有
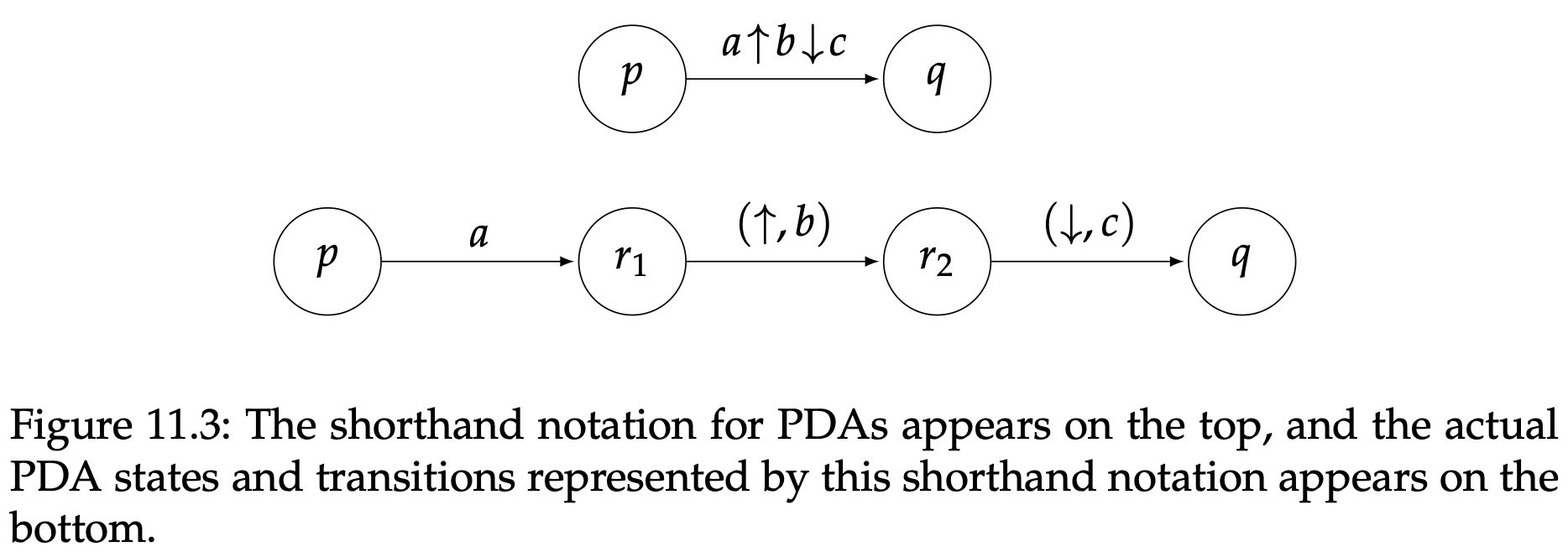
它的含义是读取符号$a$,从栈中弹出$b$,往栈中推入$c$。图11.3说明了如何理解这类简写。这种简写看起来就像是隐藏了一些状态。比如,图11.3中的$r_1,r_2$就隐藏在了$p$到$q$的转移中,不能从其他任何状态转移到达它们。
这种简写表达可以用在多个符号推入或者弹出的情况。比如,一条边标有
表示从输入中读取$a$,$b_1b_2b_3$从栈中弹出,然后将$c_1c_2c_3c_4$推入栈中。我们约定将箭头右边第一个符号当做推入或者弹出操作后的栈顶元素,这个转移要求栈顶的元素是$b_1$,它的下面是$b_2$,再往下是$b_3$ — 在整个操作执行完成之后,栈顶元素是$c_1$,然后是$c_2$,以此类推。你们可以按照图11.3来模拟这个转换过程,连通中间状态在正确的顺序下执行操作。
最后,我们可以简单地省略没有使用的部分。比如,标有
的转移表示“从输入中读取$a$,从栈中弹出$b$,不推入符号”,标有
的转移表示“不从输入读取符号,从栈中弹出$b$,然后推入$c_1c_1$”,等等。图11.4展示了图11.2中PDA的简写形式。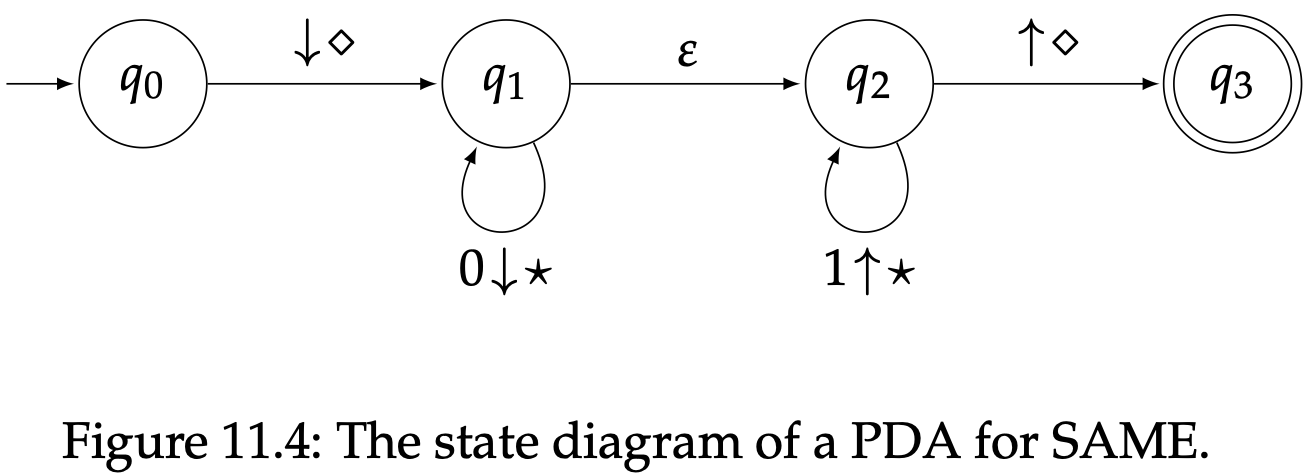
关于确定性下推自动机
必须强调的是默认情况下下推自动机都被认为是非确定性的。
定义一个确定性PDA模型是可能的,但是这样做,我们得到的是一个严格的弱计算模型。也就是说,每个确定性PDA都会识别一个上下文无关语言,但是默写上下文无关语言不能被确定性PDA所识别。基于字母表$\Sigma=\{0,1\}$的回文语言PAL就是一个例子;这个语言能被图11.5中的PDA识别,但是不存在能识别它的确定性PDA。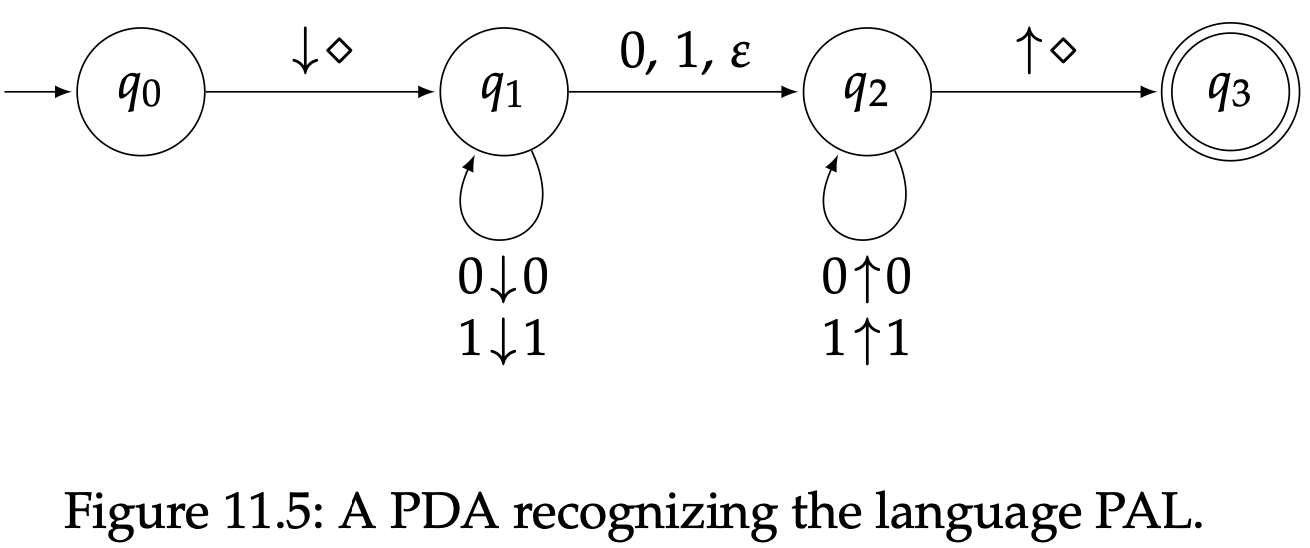
我们将不会证明这个事实,主要是因为我们根本没讨论过确定性PDA的正式定义,但是靠感觉就足够的。确定性PDA不能检测到我们是否已经到达一个字符串的中间,由于这个原因使用一个栈不足以识别回文;不管你怎么做,这个自动机永远不会知道什么时候停止推入和开始弹出。然而一个非确定性自动机通过简单的猜测就能做到这一点。
进一步的例子
接下来我们会考虑上下文无关语言更多的闭合运算。包括字符串的翻转,与有限语言的对称差,在字母表中插入和删除一个确定的符号。
翻转
我们在第六节课中已经讨论过字符串的反转了,也知道一个正则语言的翻转总是正则的。这个理论用在上下文无关语言也是正确的,来看看下面这个命题构造。
命题11.3. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个上下文无关语言。语言$A^R$是上下文无关的。
证明:因为$A$是上下文无关的,一定存在一个CFG $G$使得$A=L(G)$。定义一个新的CFG $H$如下:$H$包含和$G$中一样的的变量,对于$G$的每条规则$X\rightarrow w$,加入一条$X\rightarrow w^R$到$H$中。用文字表达就是$H$规则就是将$G$中的每条规则左右翻转得到。很明显$L(H)=L(G)^R=A^R$,因此$A^R$是上下文无关的。
与有限语言的对称差
接着我们来看对称差,这个也在第六节课中定义过。当然任意两个上下文无关语言的对称差并不总是上下文无关的,甚至一个上下文无关语言和一个正则语言的对称差也不总是上下文无关的。
比如,如果$A\subseteq\Sigma^{*}$是上下文无关的,但$\overline{A}$不是,那么$A$和$\Sigma^{*}$的对称差就不是上下文无关的,因为
另外,一个上下文无关语言和一个有限语言的对称差总是上下文无关的,命题在后面。这就很有趣了,因为一个已知语言和一个有限语言的对称差有直观上的意义:它表示我们在更改一个语言中有限数量的字符串,要么包含,要么排除这些字符串。因此这个命题告诉我们修改一个语言中优先数量的字符串并不会破坏它的属性。
命题11.4. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个上下文无关语言,$B\subseteq\Sigma^{*}$是一个有限语言。语言$A\Delta B$是上下文无关的。
证明:首先,已知$B$是有限的,我们知道$B$是正则的,因此$\overline{B}$也是正则的因为正则语言在补集运算下是闭合的。这表示$A\cap \overline{B}$是上下文无关的,因为一个上下文无关语言和一个正则语言的交集是上下文无关的。
接下来,我们知道$\overline{A}\cap B$包含于$B$,因此它是有限的。每个有限语言都是上下文无关的,因此$\overline{A}\cap B$是上下文无关的。
最后,我们已经证明过$A\cap \overline{B}$和$\overline{A}\cap B$都是上下文无关的,那么$A\Delta B=(A\cap \overline{B})\cup (\overline{A}\cap B)$是上下文无关的,因为两个上下文无关语言的并集必须是上下文无关的。
字符串映射下的闭包
假设$\Sigma$和$\Gamma$是不相交的字母表集合,我们有一个字符串$w\in(\Sigma\cup\Gamma)^{*}$,它包含的符号来自于这两个字母表。我们可以想象删除$w$中来自于$\Gamma$的符号,会留下一个基于$\Sigma$的字符串。我们将这个操作称作一个基于字母表$\Sigma\cup\Gamma$的字符串到字母表$\Sigma$的映射。
我们将会证明上下文无关语言关于这个概念的两个闭包属性。第一个讲的是如果你有一个基于字母表$\Sigma\cup\Gamma$的上下文无关语言,然后将这个语言$A$中的字符串映射到字母表$\Sigma$,你会得到一个上下文无关语言。
命题11.5. 已知$\Sigma$和$\Gamma$是不相交的字母表,$A\subseteq(\Sigma\cup\Gamma)^{*}$是一个上下文无关语言,定义
语言$B$是一个上下文无关的。
证明: 因为$A$是上下文无关的,一定存在一个乔姆斯基范式CFG $G$使得$L(G)=A$。我们构造一个新的CFG $H$如下:
- 对于$G$中每条形如$X\rightarrow \Upsilon Z$的规则,把它加入到$H$中。当然规则$S\rightarrow\varepsilon$也同样处理。
- 对于$G$中每条形如$X\rightarrow a$的规则,其中$a\in \Sigma$,把它加入到$H$中。
- 对于$G$中每条形如$X\rightarrow b$的规则,其中$b\in \Gamma$,加入规则$X\rightarrow \varepsilon$到$H$中。
显然$L(H)=B$,因此$B$是上下文无关的。
这个命题反过来也是对的,打个比方:如果$A$是一个基于字母表$\Sigma$的上下文无关语言,我们考虑一个基于字母表$\Sigma\cup\Gamma$的语言,它的字符串可以映射到字母表$\Sgima$,得到语言$A$,那么这个基于字母表$\Sigma\cup\Gamma$的语言也是上下文无关的。本质上,这个语言中的字符串就是通过选取一个$A$中的字符串,然后往任意位置插入任意数量的$\Gamma$中的符号得到。
命题11.6. 已知$\Sigma$和$\Gamma$是不相交的字母表,$A\subseteq\Sigma^{*}$是一个上下文无关语言,定义
语言$B$是上下文无关的。
证明:因为$A$是上下文无关的,一定存在一个乔姆斯基范式CFG $G$使得$L(G)=A$。定义一个新的CFG $H$如下:
- 对于每个$b\in\Gamma$加入规则到$H$中,对于还未在$G$中使用的新变量$W$再加入一条$W\rightarrow \varepsilon$。变量$W$生产符号来自$\Gamma$的字符串,包括空字符串。
- 对于$G$中每条形如$X\rightarrow \Upsilon Z$的规则,不改动,把它加入到$H$中。
- 对于$G$中每条形如$X\rightarrow a$的规则,加入规则到$H$中。
- 如果$G$中有$S\rightarrow \varepsilon$这条规则,加入规则到$H$中。
直观来说,$H$的运作方式和$G$一样,除了$G$在生成一个字符或者空字符串时,$H$也生成同样的字符串,但是会往里面插入任意数量的$\Gamma$中的符号。我们得到$L(H)=B$,因此$B$是上下文无关的。
PDA和CFG的等价
正如我们在这节课早前提到的,一个语言是上下文无关的当且仅当它能被一个PDA识别。这部分我们会提供一种方式来证明这个等价。
每个上下文无关语言都能被一个PDA识别
为了证明每个上下文无关语言都能被一个PDA识别,我们为一个已知的CFG定义一个PDA。也就是,如果
是一个上下文无关语法,那我们我们能得到一个PDA $P$使得$L(P)=L(G)$,如图11.6所示。栈的字母表是$V\cup \Sigma$,加上一个栈底标识$\diamondsuit$,在计算过程中栈提供了一种方式来存储符号和变量来执行$G$的推导。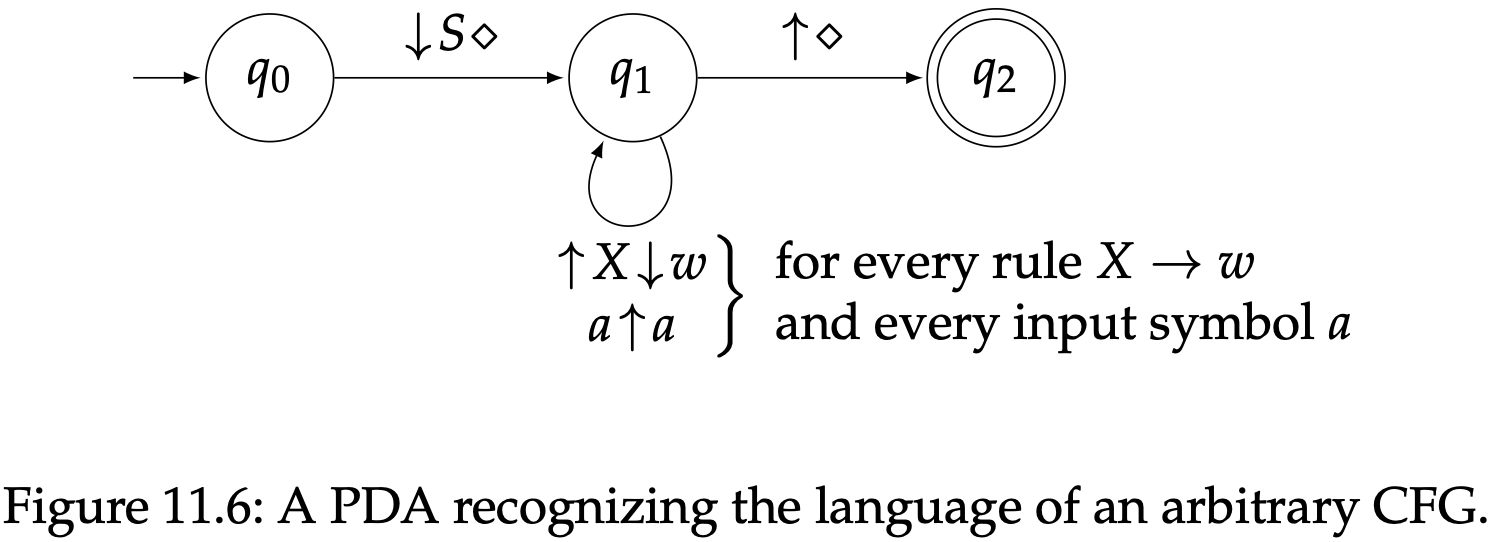
如果你在思考语法$G$的字符串是怎么推导以及操作所对应的PDA $P$又是如何工作的,那么很明显$P$能接受$G$所生成的字符串。我们一开始的栈顶元素是初始变量(另外栈底标识在下面)。一般而言,如果一个变量出现在栈顶,我们就将它弹出,然后推入它所处规则右边的符号和变量;如果一个符号出现在栈顶,我们就将它与一个输入符号比较 — 只要输入符号和这个符号一样,我们就将这个符号弹出栈外,然后移动到下一个输入符号,接着继续处理栈顶元素。我们可以移动到接受状态仅当栈为空的时候(就是只剩下一个栈底标识的时候),而且所有输入符号都被读取了。这种情况就是典型的输入字符串通过这个语法推导出来了。
每个能被PDA识别的语言都是上下文无关的
现在我们来讨论每个被PDA识别的语言都是上下文无关的。有一个方法可以将一个已知PDA转变成一个等价的CFG,但它是很混乱,而且细节部分还会让人疑惑。这里我们会总结一种不同的方式来证明每个能被PDA识别的语言都是上下文无关的,而且相当简单,想想我们在学习上下文无关语言过程中所使用的方法。如果你想,你可以将这个证明转变为为一个已知PDA构造一个CFG,这和我们刚才所提到的方法没有太大的差别,但是我们将更着重于证明而不是明确的构造。
假设我们有一个PDA $P=(Q,\Sigma,\Gamma,\delta,q_0,F)$。转移函数$\delta$的形式为
所以如果我们想的话,我们能把$P$想成是某个基于$\Sigma\cup\updownarrow\Gamma$的语言的NFA。稍微正式一点,让$N$表示这个NFA,它的定义是
我们都没有必要改变转移函数,因为NFA的转移函数正好是基于字母表$\Sigma\cup\updownarrow\Gamma$。还要定义能被$N$识别的语言$B=L(N)\subseteq(\Sigma\cup\updownarrow\Gamma)^{*}$。一般而言,$B$中的字符串同时包含了$\Sigma$和$\updownarrow\Gamma$的符号。即便所有出现$\updownarrow\Gamma$的符号的字符串都能被$N$接受,也不能说明这些字符串是有效栈字符串,因为$N$没有栈来检测这个条件。
现在让我们考虑第二个语言$C\subseteq(\Sigma\cup\updownarrow\Gamma)^{*}$。这个语言的字符串都基于字母表$\Sigma\cup\updownarrow\Gamma$,还有个条件删除任意字符串中所有$\Sigma$的符号,就会得到了一个有效栈字符串。我们已经知道由有效栈字符串构成的语言是上下文无关的,根据命题11.6,$C$也是上下文无关的。
接下来,我们考虑交集$D=B\cap C$。因为$D$是一个正则语言和一个上下文无关语言的交集,它是上下文无关的。而$D$中的字符串正好能满足PDA $P$到达接受状态;但是此外如果输入符号属于$\Sigma$则会被$P$读取,字符串中属于$\updownarrow\Gamma$的符号则代表着$P$转移过程中的栈操作。
将语言$D$中所有$\updownarrow\Gamma$的符号删除得到语言$A$,因为我们知道$D$是上下文无关的,根据命题11.5,$A$也是上下文无关的,我们想要的证明完成了。